Patient-specific Digital Heart for Arrhythmia Ablation
Overview of the Process
The aim is to develop a digital twin of a patient's heart that can simulate its electrical activation behaviors, to assist physicians during atrial arrhythmia ablation surgeries.
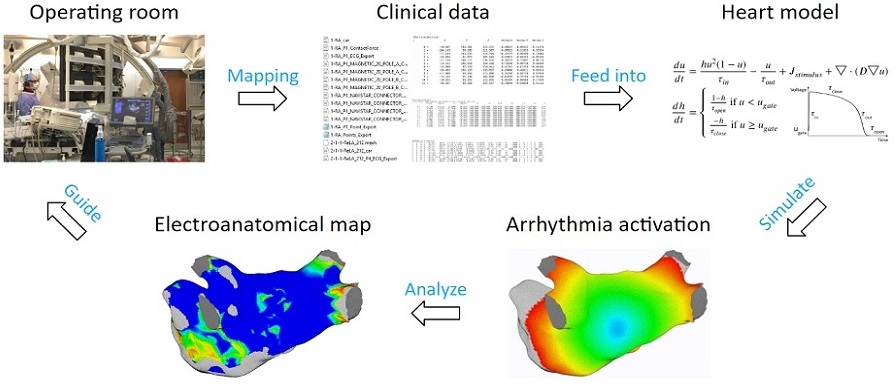
The process begins by extracting patient data to tune heart model parameters, followed by initiating arrhythmia according to patient data. Then the heart model equations are solved to simulate patient-specific arrhythmias.
Heart Model Equations
The heart model equations calculate activation action potentials. Some parameters affect the shape of the action potential, while others affect activation propagation. These parameters are tuned locally. Each vertex of the mesh has its own set of parameter values.
To solve the heart model equations, the left atrium is spatially discretized by transforming the 3D triangular mesh into a set of Cartesian nodes. For each mesh vertex, Cartesian nodes are generated within a specified radius. Repeating this process for all vertices produces a distribution of Cartesian nodes that wraps around the mesh surface.
The heart model equations are discretized in time using the explicit Euler method. With some initial values at time zero, the values for the next time step can be computed.
To compute the diffusion term, no-flux boundary conditions are applied. A 19-node stencil is used, where the action potential of the red node is diffused into its 18 neighbors according to the diffusion coefficient matrices.
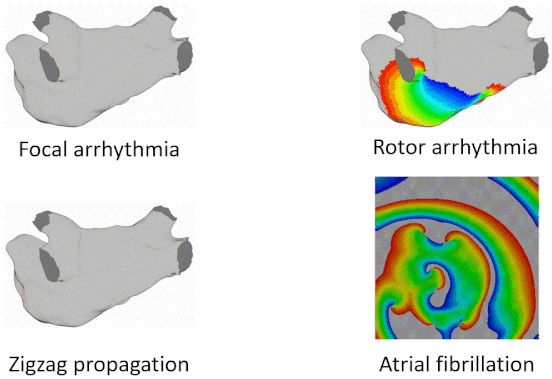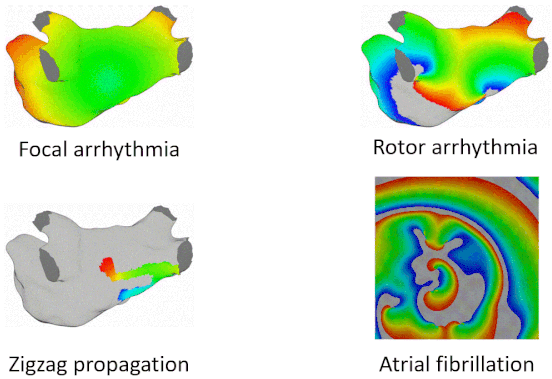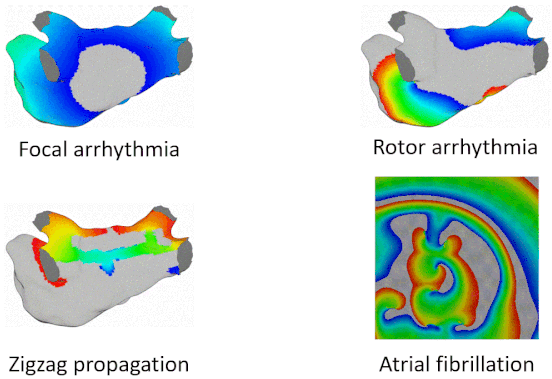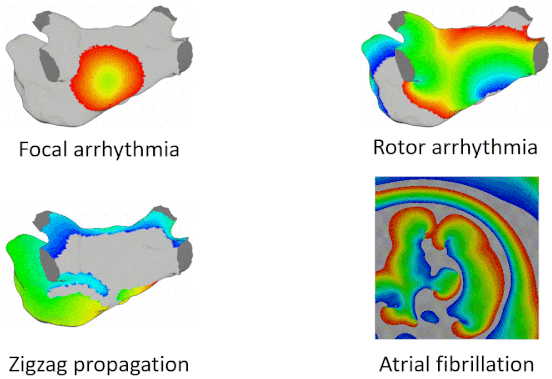
Examples of Arrhythmia Simulations
Here are examples of arrhythmia simulations. Focal arrhythmia: Activation originates at an abnormal location. Rotor arrhythmia: Spiral waves cause irregular heartbeat. Zigzag propagation: Complex scar distributions create activation tunnels of various conduction velocities. Atrial fibrillation: Chaotic activation waves that have no organizations.
Diffusion Coefficient Tuning
The solution to the lack of fiber data is to compensate for it through diffusion coefficient tuning. Tuning is challenging: 1) Heart model is nonlinear. 2) Diffusion is influencing the neighbor nodes, not the immediate vicinities. 3) Sensitive to the initial guess values, adjustment steps, ending criteria, etc.
An optimization process was developed to overcome these challenges. Patient data are processed to obtain the true local activation times. A simulation is then run with an initial guess of diffusion values, and simulated local activation times are extracted. The two sets of activation times are compared, and diffusion values are updated accordingly. This iterative process continues until the difference between patient activation times and simulation activation times is minimized.
To accelerate tuning, the relationship between conduction velocity and diffusion coefficient is exploited, reducing the number of iterations required to reach the optimum. Scar regions are accounted for in the process. In the figure below, scar regions are shown in red on the left, and the diffusion coefficient map is shown on the right, with red representing low conductivity. The red regions in both figures are almost identical, demonstrating accurate tuning.
Model Accuracy
The model achieved high accuracy in simulating arrhythmias. Experiments were conducted on seven patients’ left atria. For focal arrhythmia, an activation time accuracy of 96% was achieved.
For rotor arrhythmia, an activation time accuracy of 93% was achieved.
The model was further tested with 15 patient datasets to demonstrate the ability to reproduce patient arrhythmias accurately. The figures below show the results of 7 atrial tachycardia maps. An average activation time error of 10.97 ms was achieved, with an average correlation of 0.81.
These are the results of 8 sinus rhythm maps. An average activation time error of 5.47 ms was achieved, with an average correlation of 0.95. Sinus rhythm maps are helpful: oftentimes, a patient comes into the operating room in sinus rhythm, or undergoes cardioversion into sinus rhythm, to acquire a voltage map for assisting pulmonary vein isolation.